Java的位运算

wuxuan.chai

Java

发布于：2021年1月19日

次浏览

Java的位运算

基础概念

位：表示二进制位。是二进制计数系统中用来表示小于2的整数，一般用0或者1表示，是具有相等概率的两种状态的一种，二进制位的位数可以表示一个机器字的字长，一个二进制包含的信息量称之为1bit。

原码：二进制的定点表示法，即高位为符号位，’0’ 表示为正，’1’ 表示为负，其余位表示数值大小。

反码：正数的反码与其原码相同；负数的反码是对正数逐位取反，符号位保持为1。

补码：正数的补码与其原码相同，负数位的补码是在其反码的末位加1。

Practice

为什么java中的int类型的值取值范围为：-2³¹ ~ 2³¹-1 ？

Integer占用4byte，1byte占用8bit：
最大的正数原码：01111111 11111111 11111111 11111111
最小的负数原码：10000000 00000000 00000000 00000000
计算机存使用的都是补码：
最大的正数的补码：
01111111 11111111 11111111 11111111 -> 2³¹-1
最大的负数的补码：
11111111 11111111 11111111 11111111 +1 -> -2³¹-1 + 1 = -2³¹

原码、反码、补码的产生、以及应用

在自然界中，我们计数一般都是从正数计数，比如、一棵树、两头牛、三只羊….不存在负一棵树、负两头牛、负三只羊…都是我们在生产生活中，加入了统计之后才引入了负的概念。

在上面我们了解到，正数的原码、反码、补码都是相同的，而负数的反码是原码的取反，补码是反码+1。是不是觉得反码是针对负数设计的呢？哈哈。。

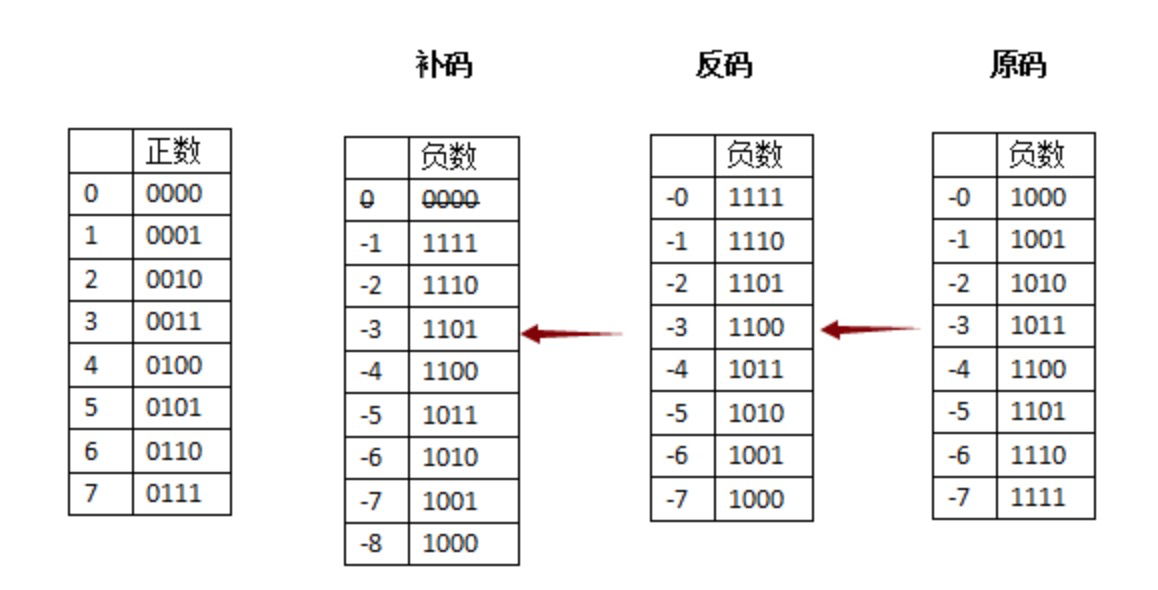
在计算机中如何处理 -7 + 7 = 0的计算呢？

以4BIT的数为例，高位作为符号位：
如果从原码的角度->
-7： 1111
7： 0111
如果拿原码做加法计算的话： 1 0110 高位舍去-> 0110 = 6 结果很显然错了！
如果从反码的角度->
-7: 1000
7: 0111
如果拿反码做加法计算的话： 1111 = -7 结果很显然也是错的！
如果从补码的角度->
-7: 1001
7: 0111
如果拿补码做加法计算的话： 1 0000 丢到高位的符号位，结果为0 看结果就是这么巧合！！！
综上，补码是做加减法最好的选择。

说到现在，是不是觉得补码就是为了计算而设计的呢？哈哈。。。

位运算

关于位运算，这里运用哲学上三个究极问题试图讲解清楚位运算究竟是何方神圣：什么是位运算？位运算的作用？位运算有什么优势？

什么是位运算？

程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如，and运算本来是一个逻辑运算符，但整数与整数之间也可以进行and运算。举个例子，6的二进制是110，11的二进制是1011，那么6 and 11的结果就是2，它是二进制对应位进行逻辑运算的结果（0表示False，1表示True，空位都当0处理）。
下表列出了位运算符的基本运算:
假设：两个4bit的数，高位表示符号位，A=3，B=7
bit(A)= 0011 bit(B)= 0111

运算符	描述	例子
按位与（&）	如果相对应位都是1，则结果为1，否则为0	A&B=3，即 0011
按位或（｜）	如果相对应位都是0，则结果为0，否则为1	A\|B=7, 即 0111
按位异或（^）	如果相对应位值相同，则结果为0，否则为1	A^B= 4, 即 0100
按位取反（~）	按位取反运算符翻转操作数的每一位，即0变成1，1变成0	~A=-4, 即 1100
左移（<<）	按位左移运算符。左操作数按位左移右操作数指定的位数	A<<2=-4, 即 1100
右移（>>）	按位右移运算符。左操作数按位右移右操作数指定的位数	B>>2=1, 即0001

位运算的作用？

位运算其实在我们日常开发过程中经常会忽略掉，因为我们习惯了使用int或者long值进行计算，而忽略了底层的计算逻辑。找一个使用了位运算的代码研究下：copy自java.long.Integer的静态方法

/**
 * 返回一个int值，最多一个1位，位于指定int值的最高("最左")1位的位置。如果指定的值在其2的补码二进制表示中没有1位，也就是说，如果它等于0，则返回0。.
 *
 * @param i the value whose highest one bit is to be computed
 * @return an {@code int} value with a single one-bit, in the position
 *     of the highest-order one-bit in the specified value, or zero if
 *     the specified value is itself equal to zero.
 * @since 1.5
 */
public static int highestOneBit(int i) {
    // HD, Figure 3-1
    i |= (i >>  1);
    i |= (i >>  2);
    i |= (i >>  4);
    i |= (i >>  8);
    i |= (i >> 16);
    return i - (i >>> 1);
}

方法流程：

public static int highestOneBit(int i) {
    //输入的i = 17  ->  00000000 00000000 00000000 00010001
    int left = i >> 1; // 00000000 00000000 00000000 00001000
    i = i | left;   //00000000 00000000 00000000 00011001   1 +8 +16 = 25
    left = i >> 2; //00000000 00000000 00000000 0000110
    i = i | left; //00000000 00000000 00000000 00011111  1+2+4+8+16 =31
    left = i >> 4;//00000000 00000000 00000000 00000001
    i = i | left; //00000000 00000000 00000000 00011111 31
    left = i >> 8; //00000000 00000000 00000000 00000000
    i = i | left;  // 00000000 00000000 00000000 00011111
    left = i >> 16; //00000000 00000000 00000000 00000000
    i = i | left; //00000000 00000000 00000000 00011111  1+2+4+8+16 = 31
    final int i1 = i >>> 1; //00000000 00000000 00000000 00001111 1+2+4+8=15
    return i-i1; // 31 -15 = 16
}